本記事をご覧の方は、つるかめ算の出題傾向や解き方について、「つるかめ算とは何か。」「つるかめ算は中学受験で頻出なのか。」「どのように解けば良いのか。」など、さまざまな疑問や悩みを抱えていらっしゃるのではないでしょうか。
本記事では、つるかめ算について以下5点を解説していきます。
- つるかめ算の特徴、学習タイミングや出題傾向
- つるかめ算の基本的な解法
- 応用的なつるかめ算
- つるかめ算の出題パターン(練習問題)
- つるかめ算を効果的に学習するためのステップ
本記事をご覧いただければ、つるかめ算の正しい解き方や効率的な学習方法を理解し、算数の得点アップにつなげられます。
中学受験に向けて計算力や論理的思考力を伸ばし、志望校合格に一歩近づけるよう、ぜひ参考にしてください。
目次
つるかめ算とは

つるかめ算とは「つるの足」と「かめの足」のような数が異なるものについて、それぞれの数を計算や図、表などで求める問題です。小学校の教科書には登場しないものの、中学受験で頻繁に出題されるため独自の対策が必要になります。
つるかめ算の基本的な問題は、以下のとおりです。
| つる、かめが合わせて10匹います。足の合計本数は24本です。かめは何匹いるでしょう。 |
つるかめ算には「つる」と「かめ」だけでなく、値段の異なる果物や切手、文房具なども登場します。入試では、割合や速さなど他単元と組み合わせて出題する学校もあり、解き方もさまざまです。
つるかめ算を学習する際は、どのような問題パターンがあるのかを理解し、適切な解法を瞬時に見極められるように練習を重ねましょう。
つるかめ算はいつ習うのか

2017年に告示された現行の学習指導要領には、つるかめ算に関する記述がないため、小学校では「つるかめ算」は単元としては存在しません。しかし、先生によっては授業で取り扱ったり、中学受験では頻繁に出題されることから、学習塾では4〜5年生の授業で扱うパターンが多く見られます。
学習塾に通っていない方も、中学受験をする場合は四則計算をマスターしている4年生からつるかめ算を勉強するのがおすすめです。入試では、割合や速さなどの問題と組み合わせたつるかめ算も出題されるため、他単元の内容も確実に習得しつつ、正しい解き方を覚えましょう。
中学受験につるかめ算は出題される

つるかめ算は中学受験で頻出の単元です。必ず出題されるとは限りませんが、解けるかどうかで合否が決まる場合もあるため、さまざまな問題パターンや解法を身につけておく必要があります。
まずは、つるかめ算の中学受験における位置づけや近年の出題傾向を把握し、学習するときに意識すべきポイントを押さえましょう。
つるかめ算の位置づけ
つるかめ算は単純な計算力だけでなく、問題場面から答えまでの道筋を立てる論理的思考力を測る目的として出題されます。そもそも中学受験では、基礎知識が身についていることを前提とした応用的な問題を出題する傾向にあるためです。
入試では、基礎知識を組み合わせる問題を出すことで、思考力・判断力・表現力や問題解決能力の有無を確かめます。つるかめ算でも、複雑な条件が提示されたり他単元と組み合わせたりした問題が出題されるでしょう。
そのため、つるかめ算の学習では計算方法を暗記するだけでなく、その解法が成り立つ理由や仕組みを理解すると、問題形式が変わっても対応できるようになり、得点アップにもつながります。
出題傾向の変化
つるかめ算には基本の解法パターンが数種類あります。シンプルな問題であれば、基本的な解法を覚えることで簡単に答えを求められるでしょう。
しかし、それでは論理的思考力や問題解決能力を正しく測れません。そのため難関校では、以下のような応用的な問題が出題される傾向にあります。
| 花子さんは 1 個 80 円のりんご、1 個 120 円の梨、 1 個 160 円の柿を合わせて 46 個買ったところ、代金は 6160 円でした。花子さんが買ったりんごと柿の個数の比が 1:3 のとき、梨の個数は__個です。 |
参考元:青山学院中等部 2024年度入試問題(算数)丨青山学院中等部
難易度の高い応用問題を解くためには、つるかめ算だけでなく他単元の概念や公式も確実に習得するなど、算数全体のスキルアップを図ることが大切です。
つるかめ算を学習する意義
つるかめ算は中学受験の算数において重要度の高い単元ですが、小学校で習う機会がないため独自の対策を進める必要があります。
つるかめ算の解法を習得する際は、なぜその計算ができるのかを徹底的に理解しましょう。長い文章問題でも、条件整理や適切な解法の見極めがすぐにできるレベルまで読解力を鍛えるのもおすすめです。
暗記だけに頼らず論理的思考力の育成に重点を置くことで、対応できる問題の幅が広がり他の受験生に差をつけられます。
つるかめ算の基本的な解法

つるかめ算は式や表、面積図を使って解くのが基本です。また中学校で習う連立方程式の土台となるため、方程式も解法として使えます。
ここでは、つるかめ算の基本的な解法について以下の例題をもとに見ていきましょう。
| つるとかめが合わせて100匹います。足の数が全部で296本のとき、つるとかめはそれぞれ何匹いるでしょう。 |
慣れるまでは問題場面を図に表したり、一つずつ手順を追ったりしながら解法パターンを身につけることが大切です。
式を使ったつるかめ算の解法
式を使ったつるかめ算の解法では、まず「全部をつる(または全部をかめ)」と仮定します。つるが100匹いると仮定した場合、全体の足の数は以下のとおりです。
| 足2本×つる100匹=200本 |
しかし問題文には「足の数が全部で296本」とあり、これでは96本足りません。そこで、つるとかめの足の本数に注目しましょう。
つるの足は2本、かめの足は4本あるため、その差は2本です。つまり、つる1匹をかめ1匹に置き換えれば全体の足の本数が2本増えます。足りない分の96本を2で割ると、必要なかめの数がわかります。
| 96(足りない本数)÷2(つるとかめの足の数の差)=48(かめの数) |
全体(100匹)からかめの数を引いた結果、つるの数は52匹です。
| 全体100匹-かめ48匹=52匹 |
上記から、答えは「つる52匹、かめ48匹」となります。
全部をかめと仮定した場合も考え方は同じです。全部をどちらか一方にした上で式を立てると、異なるもの同士の数の差から答えを求められます。
表を使ったつるかめ算の解法
表を使った解法では、以下のように「つるの数」「かめの数」「足の合計」の項目を設定し、全部をつるだと仮定して順に数を当てはめます。
| つるの数(匹) | 100 | 99 | 98 | 97 | ・・・ | 52 |
| かめの数(匹) | 0 | 1 | 2 | 3 | ・・・ | 48 |
| 足の合計(本) | 200 | 202 | 204 | 206 | ・・・ | 296 |
この方法を使えば着実に答えまでたどり着けますが、大きい数を扱う場合は表を埋めるのに時間を要する点がデメリットです。そこで、表を埋めながら数の法則を見つけることを意識しましょう。
例題からは「つるをかめに1匹変換させるごとに足の合計が2本ずつ増える」という法則を見つけられます。つまり足の合計を296にするためには「(296-200)÷2=48」から、48匹のかめが必要です。かめの数がわかれば「100-48=52」でつるの数も出せます。
同じように全部をかめだと仮定して表を作成する場合は、「かめをつるに1匹変換させるごとに足の合計が2本ずつ減る」という法則を見つけられるはずです。
面積図を使ったつるかめ算の解法
面積図を使うと数量関係を視覚化できるため、直感的に問題を解くことができます。図形が苦手なお子さんは難しく感じられるかもしれませんが、面積図を使いこなせば速さや食塩水の問題も内容をイメージしやすくなり、論理的に答えを出せるでしょう。
例題を面積図にすると、以下のように表せます。
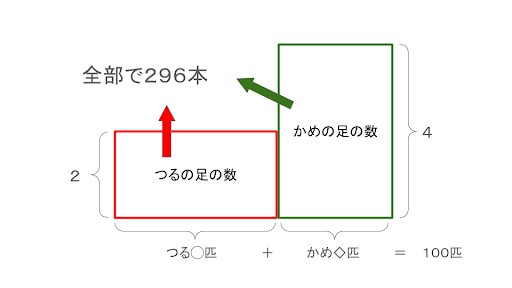
つるとかめの数を横の長さ、1匹あたりの足の数を縦の長さで表すと「縦2の長方形」と「縦4の長方形」ができます。2つの長方形の面積が表しているのは「つる◯匹分の足の数」と「かめ◇匹分の足の数」です。そのため、長方形の面積を合わせると、全部の足の数である「296」になります。
つるとかめの数を求めるには、2つの長方形を上下に分けて計算しましょう。
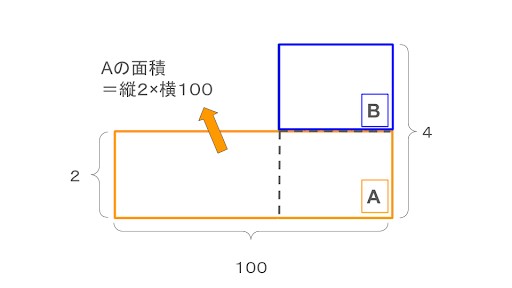
長方形Aは、縦と横の長さがわかっているため、以下の式で面積を求められます。
| 長方形A:縦2×横100=200 |
長方形Bは、面積を合計した296から長方形Aの面積を引いて求めましょう。
| 長方形B:296-200=96 |
長方形Bの縦の長さは「4-2=2」です。面積と縦の長さを使うことで、長方形Bの横の長さ(かめ◇匹)を割り出せます。かめの数がわかれば、つるの数を求めるのも簡単です。
| 長方形B:縦2×横◇(かめの数)=96 ◇=48 【つるの数を求める】 つる◯匹+かめ48匹=100匹 つる◯匹=100-48=52 |
このように縦と横の数字を正しく割り当てれば、それぞれの数字が何を意味するのか、どのような関係にあるのかを理解しながら効率的に問題を解くことができます。
方程式を使ったつるかめ算の解法
中学校で習う数学の知識を活用すれば、連立方程式でつるかめ算を解くことも可能です。
例題の場合、以下2つの方程式が成り立ちます。
| つるの数+かめの数=100匹…① 1匹あたりの足2本×つるの数+1匹あたりの足4本×かめの数=296本…② |
つるの数をa、かめの数をbとすると、以下のように式を整理できます。
| a+b=100…① 2a+4b=296…② |
①、②を連立方程式とした解き方は以下のとおりです。
| 【①の両辺を2倍する】 2a+2b=200 【式同士の足し算・引き算をする「加減法」を用いて②-①をする】 2b=96 【両辺を2で割る】 b=48(かめの数) 【bを①に代入してaを求める】 a=100-48=52(つるの数) |
上記から「つるの数は52匹、かめの数は48匹」だとわかります。連立方程式でつるかめ算を解く際は、aやbなど文字の前にかかっている「係数」を2つの式でそろえること、式同士の計算で「+」「-」などの符号間違いに気をつけることを意識しましょう。
応用的なつるかめ算

つるかめ算の特徴は、数が異なる2つのものを合計した数がわかった上で、それぞれの配分を求めることです。
ここでは、つるかめ算の仕組みを応用した5つの問題形式を紹介します。
- 弁償算
- 割合のつるかめ算
- 差のつるかめ算
- 3段つるかめ算
- いもづる算
応用的な解き方も習得すれば、幅広いパターンのつるかめ算に対応できるようになり、試験でも確実に点数を取れるでしょう。
弁償算
弁償算とは、問題場面の中でマイナスが発生するつるかめ算のことです。具体的には、以下のような問題が出題されます。
| Aさんはガラスのお皿を50枚運びます。1枚運ぶごとに10円もらえますが、お皿を割ってしまうと1枚あたり60円弁償することになります。Aさんはすべてのお皿を運び終わり、290円もらいました。割らずに運べたお皿と、割ったお皿はそれぞれ何枚でしょう。 |
弁償算は面積図でも解けますが、かえって難しくなるため表を使うのがおすすめです。表を使うと、以下のように数量関係をまとめられます。
| 運べたお皿(枚) | 50 | 49 | 48 | 47 |
| 割ったお皿(枚) | 0 | 1 | 2 | 3 |
| もらったお金(円) | 500 | 430 | 360 | 290 |
もらったお金は、すべてのお皿を割らずに運べた場合の「500円」から、「弁償したお金(60円×割ったお皿の枚数)」と「もらえるはずだった報酬(10円×割ったお皿の枚数)」を引くことで求められます。
上記から、例題の答えは「割らずに運べたお皿は47枚、割ったお皿は3枚」です。
「割ったお皿が1枚増えるごとに、もらったお金が70円ずつ減る」という法則を見つければ、以下の式で答えを求められます。
| (500-290)÷70=3(割ったお皿の枚数) |
一定の条件でマイナスが発生する問題に出会ったときは、弁償算の可能性があることを意識して適切な解法を見つけましょう。
割合のつるかめ算
割合のつるかめ算とは、以下のように2つの異なる数が割合の増減によって変化する問題です。
| A、Bという2種類のバスに、今週は合計で1,582人乗りました。先週に比べるとAの乗車人数が15%増え、Bも10%増えたので全部で182人増えています。先週はAとBのバスにそれぞれ何人ずつ乗ったでしょう。 |
割合のつるかめ算は、どちらか一方の割合にそろえて計算すると答えを求められます。
AとBのバスに先週乗った人の合計は「1582-182=1400」から、1,400人です。A・Bどちらも先週に比べて10%増えたと仮定すると、2台合わせて140人増えたことになります。
しかし実際はバスに乗った人数が182人増えており、その差は42人です。本来Aに乗った人の数は15%増えていますが、計算上は10%増と仮定しているため、この42人は割合の差の5%にあたります。
上記をもとに以下の計算をすると、先週Aに乗った人の数がわかります。
| 42÷(0.15-0.1)=840 |
先週Bに乗った人の数は「1400-840=560」で560人です。
割合のつるかめ算は登場する数字が多く、問題場面を把握するのに時間がかかってしまいます。効率よく答えを出すには、いきなり計算を始めず変化の前後関係を整理した上で、何を求めるのかはっきりさせましょう。
差のつるかめ算
差のつるかめ算とは、数の差を利用して答えを出すつるかめ算です。具体的には、以下のような問題が出題されます。
| 1個40円のりんごと、1個60円のみかんを合わせて30個買ったところ、りんごの代金がみかんの代金より400円高くなりました。このとき、りんごとみかんをそれぞれ何個買いましたか。 |
差のつるかめ算では、最初に「全部をりんご(または全部をみかん)」と仮定しましょう。たとえば全部をりんごと仮定して計算すると、りんごとみかんの代金の差が1,200円だとわかります。
| 【りんごを30個買ったと仮定した場合】 40×30=12001200(りんごの代金)-0(みかんの代金)=1200 →本来の代金の差(400円)よりも800円高い |
りんご1個をみかん1個に置き換えると、「40+60=100」で100円分の差が縮まります。800円分の差を縮めるために必要なみかんの数は「800÷100=8」から、8個です。
最後に全体の個数からみかんの数を引けば、りんごの数が「22個」だとわかります。
差のつるかめ算は「合計」と「差」が同時に登場することから内容を理解しにくいため、慣れるまでは図や表をもとに問題場面を把握しましょう。
3段つるかめ算
3段つるかめ算は、以下のように計算対象が3種類になっている問題です。
| 150円のはさみ、100円のえんぴつ、30円の消しゴムを買ったところ、全部で10個買って代金は820円でした。それぞれ何個買ったでしょう。 |
3段つるかめ算を解く際は、対象物を減らして計算を楽にするのがポイントです。例題の場合、どれを買っても必ず30円はかかるため代金の820円から300円を引きます。
| 820-(30×10)=520 |
次に、はさみ・えんぴつの代金からそれぞれ30円を引いた「120円」「70円」をもとに、合計が520円になる組み合わせを考えましょう。すると答えは「はさみ2個、えんぴつ4本、消しゴム4個」となるはずです。
問題文で「はさみとえんぴつの数が同じ」「はさみはえんぴつよりも◯個多い」などの条件が提示されている場合は、表や面積図を使った方法でも答えを求められます。
いもづる算
いもづる算は、条件が少ないために複数の答えを出さなければならないつるかめ算です。基本的なつるかめ算では「単位あたりの量」「全体の個数」「全体の量」が問題文で提示されますが、以下の例題では「単位あたりの量」しかわかりません。
| 1個120円のチョコレートと1個80円のクッキーを何個か買ったところ、代金は840円になりました。チョコレートとクッキーの買い方は何通りあるでしょう。ただし、どちらも必ず1個以上買うものとします。 |
いもづる算を解く際は、文字・記号を使った式と表を活用しましょう。まず問題文をもとに「チョコレート◯個」「クッキー△個」として以下の式を立てます。
| 120円×◯個+80円×△個=840円 |
次に計算を簡単にするため、すべての項を同じ数で割りましょう。例題の場合は40で割ります。
| 3×◯+2×△=21 |
各項の数字を小さくしたら表を書き、買い方のパターンが何通りあるか見つけます。
| チョコレートの個数 | 7個 | 5個 | 3個 | 1個 |
| クッキーの個数 | 0個 | 3個 | 6個 | 9個 |
| 合計代金 | 840円 | 840円 | 840円 | 840円 |
すべてのパターンを書き出すのは手間がかかりますが、表を整理するうちに一定の法則が見えてくるはずです。例題では「どちらも必ず1個以上買うもの」と指示しているため、答えは「3通り」となります。
つるかめ算の出題パターン(練習問題)
つるかめ算の基本的な解法をもとに、以下4つの練習問題に取り組みましょう。
- 基本的なつるかめ算
- 商品の購入問題
- 損益に関する問題
- 速さに関する問題
計算に時間がかかったり、間違えたりした問題は正しい解き方を理解し、復習を繰り返して少しずつコツをつかむことが大切です。
基本的なつるかめ算
| つるとかめが合わせて23匹います。足の数を合わせると74本です。つるとかめはそれぞれ何匹ですか? |
基本的なつるかめ算は式や表、面積図や方程式などさまざまな方法で解けます。どちらか一方に仮定して解く場合は、以下の流れで計算しましょう。
| 【全部をつるだと仮定して足の本数を求める】 足2本×つる23匹=46本(28本足りない) 【足りない分をかめに置き換える】 28(足りない本数)÷2(つるとかめの足の差)=14(かめの数) 【つるの数を求める】 23(つるとかめの合計)-14=9(つるの数) |
上記から、答えは「つる9匹、かめ14匹」です。
商品の購入問題
| あめとチョコを合わせて15個買ったら、合計630円でした。あめが1個30円、チョコが1個60円だったとき、あめとチョコはそれぞれ何個ずつ購入しましたか? |
上記の問題も「1個あたりの代金」「合計の代金」「合計の個数」がわかっており、基本の解法で答えを求められます。「全部をチョコ」だと仮定した場合の解き方は、以下のとおりです。
| 【チョコを15個買ったと仮定して、代金を求める】 チョコ60円×15個=900円(270円あまる) 【あまった分の270円をあめに置き換える】 270÷30(チョコとあめの代金の差)=9(あめの数) 【チョコの数を求める】 15-9=6(チョコの数) |
よって、答えは「あめ9個、チョコ6個」となります。
つるとかめが登場しなくても、問題場面や条件から「つるかめ算かどうか」を見極めることが正しい答えを出すためのポイントです。
損益に関する問題
| 1個あたり100円で仕入れた商品200個に、4割の利益を見込んで定価をつけました。その後、売れ残ったものを定価の2割引にしたところすべて売れました。このときの利益が6600円だったとき、定価で売れた商品は何個ですか? |
上記の問題はさまざまな数字が出てくるため、以下のように条件を整理した上で式を立てましょう。
| 1個あたりの仕入値 | 100円 |
| 定価 | 100×(1+0.4)=140(1個あたりの利益は40円) |
| 値引きした値段 | 140-(140×0.2)=112(1個あたりの利益は12円) |
条件を整理できたら、定価で売れた個数をa、値引き後に売れた個数をbとして連立方程式をつくります。
| a+b=200…① 40a+12b=6600…② 【①の両辺を12倍して②から引く】 a=150(定価で売れた個数) 【①にaを代入してbを求める】 b=50(値引き後に売れた個数) |
例題では定価で売れた商品の個数を聞かれているため、答えは「150個」です。
速さに関する問題
| 家から学校までの距離は980mです。最初は分速40mで歩き、途中から分速60mで走ったところ、18分で学校に着きました。走った時間は何分でしょうか? |
速さが関係する問題は以下のような面積図を用いると、何を・どのように求めるか視覚的に理解できます。
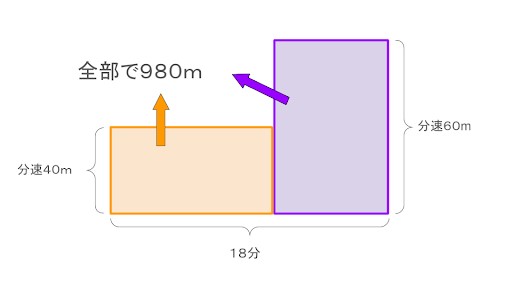
この図を上下に分け、それぞれの面積を求めれば分速60mで走った時間も割り出せます。
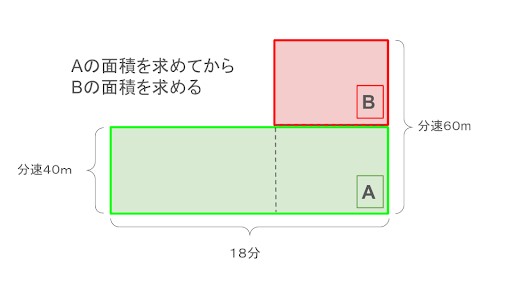
| 【長方形Aを求める】 40×18=720 【長方形Bを求める】 980-720=260 【長方形Bの横を求める】 20×(横)=260(横)=13 |
長方形Bの横は「走った時間(分)」を表しているため、答えは「13分」です。
つるかめ算を効果的に学習するためのステップ

つるかめ算にはさまざまな種類の出題形式や解法があるため、4年生で中学受験対策を始めると同時に準備を進めるのがおすすめです。具体的には、以下のステップで学習しましょう。
| 学習時期 | 学習のポイント |
| 4年生前期 | 基礎を身につける |
| 4年生後期 | 解法を定着させる |
| 5年生前期 | 応用力を育成する |
| 5年生後期 | より発展的な学習を行う |
| 6年生 | 実践的な問題を重ねる |
なぜその解法が成り立つのかを根本的に理解し、徐々にレベルを上げることで効率的に計算力や論理的思考力が身につき、他の受験生にも差をつけられます。
【4年生前期】基礎を身につける
4年生前期では、全部をどちらか一方にそろえる基本の解き方を理解することに重点を置きましょう。なぜ一方にそろえることで答えを出せるのか、一つひとつの計算にどのような意味があるのかを理解しなければ、表や面積図、方程式などを使ってもミスの可能性が高まるためです。
基本の解き方に慣れるまでは、弁償算やいもづる算などの応用ではなく初歩的な問題に取り組むことが大切です。原理を理解できたら表や面積図も使って繰り返し問題を解き、基本の解法パターンを習得しましょう。
【4年生後期】解法を定着させる
基本の解法パターンを習得できたら、次は問題場面に合わせて使い分ける練習をします。数の法則を見つけることで効率的に解ける場合は表を使う、数量関係を視覚的に表したいときは面積図を使うなど、目的に合わせて柔軟に解法を使い分けましょう。
問題場面に適した解法を選べると、計算の正確さやスピードが上がり、高得点を狙いやすくなります。一つの解法にこだわらず複数を使い分けることで、試験中に「どうやって解けば良いかわからない」と迷う場面を減らせるでしょう。
面積図や表などを使う習慣ができれば、他単元でも視覚的に問題場面を把握しやすくなるため、算数の全体的な学力アップも期待できます。
【5年生前期】応用力を育成する
5年生前期では、弁償算や割合のつるかめ算などの応用問題にも取り組み始めましょう。4年生で基礎が定着していれば、応用的なつるかめ算を解くコツもスムーズに理解できるはずです。
ただし、さまざまな解法を習得する分、出題されたときの見極めが難しくなるため、幅広いタイプの問題を解きながら「どの解法を使って答えを求めるか」を瞬時に判断する練習もしましょう。
応用的なつるかめ算には、基本的な問題と出題形式や解法が異なる部分があります。試験本番で迷わず解き進めるには「基本のつるかめ算と何が違うのか」「問題文から見分けるポイントは何か」を意識して学習することが大切です。
【5年生後期】より発展的な学習を行う
応用力が身についてきたら、差のつるかめ算・いもづる算など、より複雑な発展問題にも挑戦しましょう。
差のつるかめ算は、基本的な解法と計算の流れが似ており混同しやすい点に注意が必要です。「差」に対する理解を深め、練習を繰り返すことで基本的な解法との違いが明確になりミスを減らせます。
いもづる算は答えが複数あるため、記入漏れで失点を増やさないように正確さを重視することが大切です。
この段階では試験本番を意識し、制限時間を設けて問題を解く練習にも取り組んでみてください。
【6年生】実践的な問題を重ねる
志望校が固まっている6年生では、過去問を分析して出題傾向を把握し、弱点の補強や総合的な復習に取り組むのがおすすめです。
過去問を解く際は、本番に似た環境やスケジュールで臨むと緊張感を持てて時間配分も意識できます。「速さのつるかめ算は面積図を使う」「基本問題は得意な表を活用する」など効率的に問題を解き、点数を上げるための戦略も立てやすくなるでしょう。
過去問を解いたあとは見直しを行い、ミスの原因を徹底的に探ると考え方のクセや苦手分野が明確になり、次の学習に活かせます。実践的な問題演習を重ね、弱点やミスを確実に減らせば算数の総合的な得点アップにもつながるはずです。
まとめ

本記事では、つるかめ算の出題傾向や解き方についてご説明しましたが、特に大切なポイントは次の3つです。
- つるかめ算は中学受験で出題されやすく、計算力よりも論理的思考力や問題解決能力が求められる
- つるかめ算にはさまざまな出題形式があるため、問題場面に合わせて適切な解法を見極めることが大切
- つるかめ算を効果的に学習するには、4年生で基礎を身につけ5年生以降は応用的な問題や過去問演習で総合的なスキルを磨くと良い
つるかめ算は小学校の授業で学ぶ機会がほとんどないため、目標や計画を立てて着実にスキルアップを図りましょう。
本記事の内容をもとに、お子さんがつるかめ算の正しい解き方を習得し、志望校合格に向けて計算力や論理的思考力を磨けるよう、心からお祈り申し上げます。













