おみやげ算を使う意味はあるのか。おみやげ算を使うと計算が早くなるのか。おみやげ算を使ってどのように計算するのか。
本記事をご覧の方は、おみやげ算を使った計算方法について様々な疑問や悩みを抱えていらっしゃるのではないでしょうか。
本記事では、おみやげ算を使った計算方法について、以下5点を解説していきます。
- おみやげ算の概要
- おみやげ算を使うメリットや条件
- おみやげ算の計算方法や注意点
- おみやげ算の仕組み
- おみやげ算に似た計算テクニック
本記事をご覧いただければ、おみやげ算を使った計算方法を理解し、筆算を使わなくても効率よく計算できるようになります。
計算力や思考力を高めて算数の成績を伸ばしたい方は、ぜひ参考にしてください。
目次
おみやげ算とは

おみやげ算とは、2ケタどうしのかけ算をする際に暗算で答えを求める計算方法です。2つの数字の「十の位」が同じ数になっている場合、おみやげ算の計算方法が使えます。
おみやげ算を使った計算方法は、以下の通りです。
【13×15の場合】
- 15の一の位(5)をおみやげとして13に渡す
- 13×15が(13+5)×(15-5)=18×10(=180)になる
- 13の一の位(3)と15の一の位(5)をかける(3×5=15)
- 180と15をたす(180+15=195)
筆算が必要な問題でも、おみやげ算を使うと「2ケタ×10」や「九九」など負担の少ない計算に変換できるため、簡単に答えを求められます。
おみやげ算を使うメリット

おみやげ算を使うメリットは、以下の3つです。
- 計算スピードの向上
- 自信がつく
- 思考力の育成
おみやげ算で計算力や思考力が向上すると、学習意欲や算数に対する興味が高まり前向きに勉強を進められます。
計算スピードの向上
おみやげ算を使うと計算スピードが向上するため、解ける問題数が増えてテストでも点数を取りやすくなります。
特に中学受験では、複数の知識を組み合わせて解法を導く思考力に加え、制限時間内にすべての問題を解く計算スピードも求められます。おみやげ算で2ケタのかけ算を暗算できると短時間で最後まで解き終えることができるため、見直しの時間が増えて正答率も上がるでしょう。
また、おみやげ算は計算のスピードだけでなく正確性を高める上でも有効な手段です。複雑な2ケタどうしのかけ算を簡単な計算に直すことでケアレスミスを減らし、ライバルと差をつけられます。
おみやげ算を使える場面は限られますが、上手く活用すると正答率が高くなり、学校や塾のテストや入試でも好成績を取れます。
自信がつく
おみやげ算で複雑な計算を暗算できるようになると、算数に対する自信をつけられる点もメリットです。
おみやげ算に慣れると「25×28」や「84×82」など大きな2ケタの数どうしの暗算もできます。時間をかけて筆算していた問題も、暗算で素早く答えを出せるようになるため「周りよりも早く計算できた」「難しい問題でも簡単に答えを出せた」と自信につながるでしょう。
ただし、おみやげ算を使いこなすには「九九」や「2ケタ×10」「2ケタ×20」などの基本的な計算をマスターしなければなりません。習得には多少時間がかかるものの、おみやげ算の計算スキルが身につくと成功体験を積みやすくなり、自信を持って高度な問題にも挑戦できます。
思考力の育成
おみやげ算では頭の中で数字や計算式をイメージしながら答えを導くため、筋道を立てながら物事を考える思考力も伸ばせます。
たとえば11×18の計算をする場合、おみやげ算では以下3つの式を思い浮かべながら答えを求めます。
- (11+8)×(18-8)=19×10(=190)
- 1×8=8
- 190+8=198
おみやげ算では、上記の順序を覚えるだけでなく「どの数字を『おみやげ』として渡すのか」「何の位どうしをかけ算するのか」なども理解しなければ正しく暗算できません。
このように「何をどのように計算するのか」と計算の仕組みを考える過程で思考力が養われると、他の応用問題でも必要な知識や公式を組み合わせて論理的に答えを導けます。
おみやげ算が使える条件

おみやげ算を使うためには以下の条件が必要です。
- 2ケタどうしのかけ算であること
- 十の位が同じ数であること
- 3ケタでも使える場合がある
計算問題に取り組む際は、おみやげ算の条件に当てはまるか事前にチェックすると計算ミスを減らせます。
2ケタどうしのかけ算であること
おみやげ算は、2ケタどうしのかけ算を解く際に使うのが基本です。そのため「1ケタ×2ケタ」や「3ケタ×2ケタ」の計算でおみやげ算を使うと、間違った答えが出てしまう点に注意しましょう。
たとえば、8×16の答えは「128」ですが、以下のようにおみやげ算で計算すると「188」になります。
- 16の一の位「6」をおみやげとして8に渡す
- 8×16が(8+6)×(16-6)=14×10(=140)になる
- 8の一の位(8)と16の一の位(6)をかける(8×6=48)
- 140と48をたす(140+48=188)
「3ケタ×2ケタ」の計算をした場合も、筆算とおみやげ算では異なる答えが出ます。計算ミスを減らすためには、おみやげ算がすべてのかけ算に応用できるわけではないと理解しておくことが大切です。
十の位が同じ数であること
おみやげ算を使う際は、問題に出てくる数字の「十の位が同じ数」であることも必要です。十の位が違う数だと、おみやげ算を使っても以下のように正しい答えは出ません。
【32×15の場合(正しい答えは「480」)】
- 15の一の位「5」をおみやげとして32に渡す
- 32×15が(32+5)×(15-5)=37×10(=370)になる
- 「32の一の位(2)」と「15の一の位(5)」をかける(2×5=10)
- 370と10をたす(370+10=380)
2ケタどうしのかけ算でおみやげ算を使う場合は「32×35」や「12×15」のように、十の位が同じ数であるかどうかを確認しましょう。
3ケタでも使える場合がある
おみやげ算は、3ケタどうしのかけ算でも使える場合があります。ただし、正確な答えを出すためには以下2つの条件が必要です。
- 百の位が同じ数であること
- 十の位が0であること
106×103を例にすると、以下の手順で計算を進められます。
- 103の一の位「3」をおみやげとして106に渡す
- 106×103が(106+3)×(103-3)=109×100(=10900)になる
- 「106の一の位(6)」と「103の一の位(3)」をかける(6+3=18)
- 10900と18をたす(10900+18=10918)
本来のおみやげ算とケタ数は変わりますが、基本的な計算の順序は変わりません。おみやげ算に慣れると、3ケタどうしのかけ算でも10秒程度で答えを出せるようになります。
おみやげ算の計算方法

ここからは、おみやげ算の計算方法をいくつかご紹介します。
- 一の位が5の場合の計算方法
- 十の位が1の場合の計算方法
- 十の位が2以上の場合の計算方法
- 3ケタの場合の計算方法
おみやげ算は練習を重ねることで計算スピードや正確さを増すため、具体例を参考に自分でもさまざまな計算に取り組んでみましょう。
一の位が5の場合の計算方法
一の位が5どうしのかけ算は、他の組み合わせに比べて簡単に暗算できます。以下の2つを例に計算方法を確認しましょう。
【15×15の場合】
- 右にある15の一の位の「5」をおみやげとして、左の15に渡す
- 15×15が(15+5)×(15-5)=20×10(=200)になる
- 両方の一の位をかける(5×5=25)
- 200と25を足した225が答え
【45×45の場合】
- 右にある45の一の位の「5」をおみやげとして、左の45に渡す
- 45×45が(45+5)×(45-5)=50×40(=2000)になる
- 両方の一の位をかける(5×5=25)
- 2000と25を足した2025が答え
一の位が5どうしの場合は、おみやげを渡した後の計算が「20×10」や「50×40」とわかりやすい形になるのが特徴です。
十の位が1の場合の計算方法
十の位が1どうしの計算方法は、以下の2パターンです。
【18×19の場合(一の位が違う数)】
- 19の一の位「9」をおみやげとして18に渡す
- 18×19が(18+9)×(19-9)=27×10(=270)になる
- 一の位どうしをかけた数(8×9=72)を270にたす(=342)
【16×16の場合(一の位が同じ数)】
- 右にある16の一の位「6」をおみやげとして、左の16に渡す
- 16×16が(16+6)×(16-6)=22×10(=220)になる
- 一の位どうしをかけた数(6×6=36)を220にたす(=256)
一の位が同じ数どうしの計算については、答えを暗記するほうがスムーズに問題を解ける場合があります。自分の得意不得意に合わせて、おみやげ算を使うか答えを暗記するかを選びましょう。
十の位が2以上の場合の計算方法
おみやげ算は、十の位が同じ数であれば20以上の数どうしでも以下の方法で計算できます。
【84×82の場合】
- 82の一の位の「2」をおみやげとして84に渡す
- 84×82が(84+2)×(82-2)=86×80(=6880)になる
- 一の位どうしをかける(4×2=8)
- 6880と8をたす(=6888)
ただし、十の位が2以上の数どうしだと「86×80」のように難しい暗算をする場面が出てきます。おみやげ算を使うことで計算効率が悪くなる場合は、無理せず最初から筆算に頼るのも一つの手です。
十の位が2以上の計算に慣れるまでは、一工程ずつメモを取り正確な答えを出せるように練習を重ねましょう。
3ケタの場合の計算方法
3ケタの場合の計算方法は以下の通りです。
【203×204の場合】
- 204の一の位の「4」をおみやげとして203に渡す
- 203×204が(203+4)×(204-4)=207×200(=41400)になる
- 一の位どうしをかける(3×4=12)
- 41400と12をたす(=41412)
3ケタどうしの計算も途中で大きな数字が登場するため、暗算が苦手なお子さんは最初から筆算を使うかメモを取りながら練習しましょう。途中式を書きながら練習すると、おみやげ算のパターンや計算のコツを掴みやすくなります。
3ケタの場合のおみやげ算は使える場面が限られるため、幅広い問題に対応できるよう日頃から筆算の練習にも取り組みましょう。
おみやげ算の仕組みと証明

おみやげ算に限らず、算数では「なぜこの計算が成り立つのか」という仕組みを理解することが計算力や思考力を上げるためには大切です。
そこで、面積図を使って以下2つの場合におけるおみやげ算の仕組みを解説します。
- 十の位が1の場合
- 十の位が2以上の場合
面積図でおみやげ算の仕組みを理解できると、一つ一つの計算に意味を持たせられるためケアレスミスや計算忘れを防げます。
十の位が1の場合
たとえば「14×13」を図にすると「縦14」「横13」の四角形で表せます。(図1)
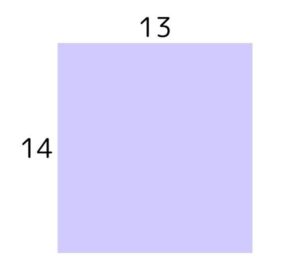
次に、横の13を10と3に分割すると「14×10」と「14×3」の2つの四角形に分けられます。(図2)
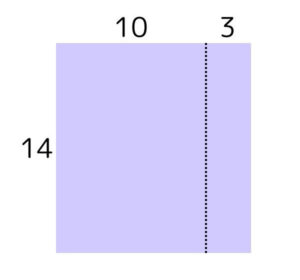
右側にある「14×3」の四角形を横に倒し「14×10」の四角形に付けた形が以下の図です。(図3)
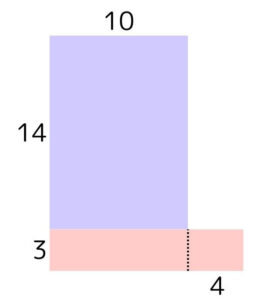
「14×13」の答えを出すためには、図3における左側の四角形と右側の飛び出した四角形の面積をそれぞれ求める必要があります。
左の四角形の面積を求める計算は(14+3)×(13-3)=17×10(=170)で、これはおみやげ算でおみやげを渡す際の計算部分です。右の四角形の面積を「3×4(=12)」で求め、最後に170と12をたすことで「14×13」の答えが出ます。
上記の手順はおみやげ算の計算方法と一致しているため、おみやげ算が成り立つと証明できます。
十の位が2以上の場合
十の位が2以上の場合も、基本的な考え方は同じです。「26×22」を例にすると、図は「縦26」「横22」の四角形で表せます。(図1)

次に、横の22を20と2に分割した形が以下の図です。(図2)
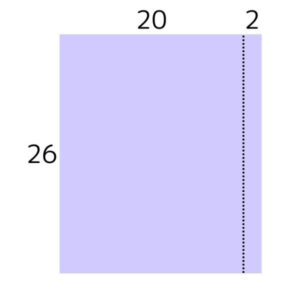
右の「26×2」の四角形を横に倒し、左の「26×20」の四角形に付けると以下の形になります。(図3)
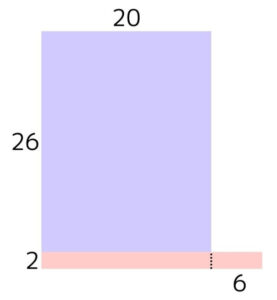
左と右の飛び出た四角形の面積をそれぞれ求め((26+2)×20、2×6)、最後に2つをたして「26×22」の答えを出す(560+12=572)のが一連の流れです。面積図を使うと、十の位が2以上の場合でもおみやげ算が成り立つことがわかります。
おみやげ算を使うときの注意点

おみやげ算を使うときは、以下のポイントに注意が必要です。
- 使えるパターンが限られている
- 算数の本質を見落とす危険性がある
- 間違えた箇所に気付きづらい
おみやげ算は計算力や思考力の向上につながる有効な手法ですが、上手に使うためには基礎学力の定着や、仕組み・概念の理解が重要であることを覚えておきましょう。
使えるパターンが限られている
おみやげ算は使えるパターンが限られており、必ずしもすべての計算で活用できるわけではありません。そのため、むやみにおみやげ算を使って失点を増やさないように気をつけましょう。
2ケタどうしのかけ算でおみやげ算を使う場合は「十の位が同じ数」になっている必要があります。3ケタどうしの場合は「百の位が同じ数」「十の位が0」であることが条件です。このように、おみやげ算は使える場面が限定されるため、せっかく計算方法を覚えてもテストで一度も使えない可能性があります。
おみやげ算を使う機会がなくても点数を取るためには、筆算でも素早く正確に計算できる力をつけることが大切です。短時間でも毎日練習を積み重ね、基本から応用まで幅広く対応できる計算力を鍛えましょう。
算数の本質を見落とす危険性がある
おみやげ算のテクニックを覚えることにのみ注力し、計算の仕組みや過程といった算数の本質を見落とす危険性がある点にも注意が必要です。
筆算を書く必要がなく速いスピードで答えを求められるおみやげ算は、お子さんにとって魅力的に感じられるかもしれません。しかし「なぜその計算が成り立つのか」という仕組みを理解しないままおみやげ算を使うことは、間違った順序で計算したり必要な計算を忘れたりする原因になります。
算数では、素早く正確に計算できる力が求められる一方、「なぜ」「どうして」という疑問をもとに算数の本質を理解する思考力も大切です。おみやげ算を使うときはテクニックだけに固執せず、仕組みにも注目しながら問題演習を繰り返し、計算方法を正しく理解しましょう。
間違えた箇所に気付きづらい
おみやげ算は暗算がメインになるため、間違えた箇所に気付きづらい可能性があります。九九や暗算が苦手なお子さんは、おみやげ算でミスを増やさないよう基本的な計算力もつけましょう。
おみやげ算は、筆算が必要な2ケタ・3ケタどうしの計算を簡単な計算に直すことで効率よく答えを求められる点がメリットです。しかし、途中式を記憶しながら計算する、「26×20」や「85×80」を暗算で解くなど高度なテクニックが求められる部分もあります。
そのため、基礎学力が定着していないお子さんがおみやげ算を使うと、正しく計算できず逆効果になる可能性があるでしょう。おみやげ算を使って計算効率を高めるには「慣れるまで途中式を書く」「かけ算の仕組みを復習する」などの方法で理解を深めることが大切です。
また、おみやげ算で間違えたときは「どこで」「なぜ」間違えたのかを分析し、復習を繰り返すことで徐々にミスを減らせます。
おみやげ算に似た計算テクニック

おみやげ算に似た計算テクニックとして、次の2つをご紹介します。
- あゆみ算
- インド式計算
おみやげ算と同様、上記の計算テクニックも「なぜ成り立つのか」を理解することが正しい答えを導くためのポイントです。
あゆみ算
あゆみ算とは、10×10〜99×99まで8100通りある2ケタどうしのかけ算を暗算する方法です。2つの数字をそれぞれ一の位と十の位に分けるため、計算の負担が軽くなりミスを減らせます。おみやげ算と異なり、十の位が違う数でも対応できる点が特徴です。
34×71を例にすると、あゆみ算では以下の図を使って答えを求めます。
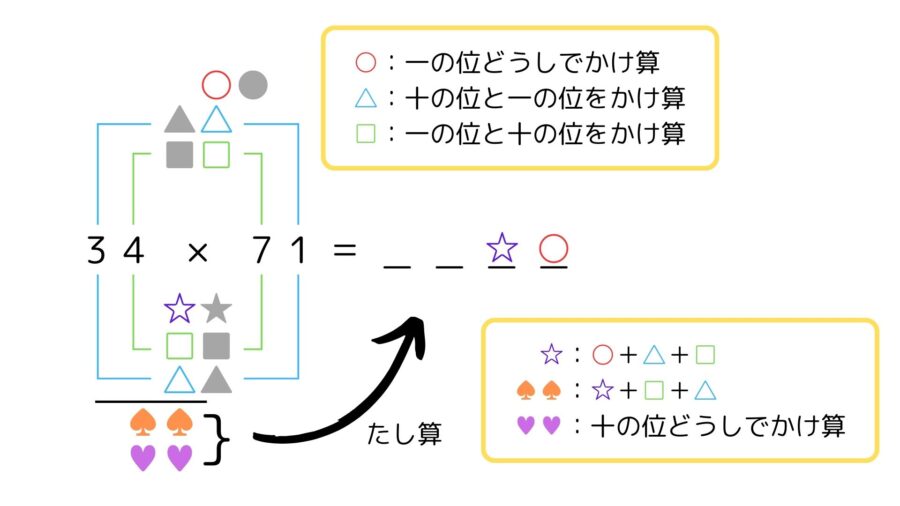
線でつないだ数どうしをかけた後、十の位と一の位を分けて記号の中に数字を書きます。かけ忘れ、たし忘れがないよう最初のうちは慎重に計算しましょう。
なお、計算結果は以下の通りです。
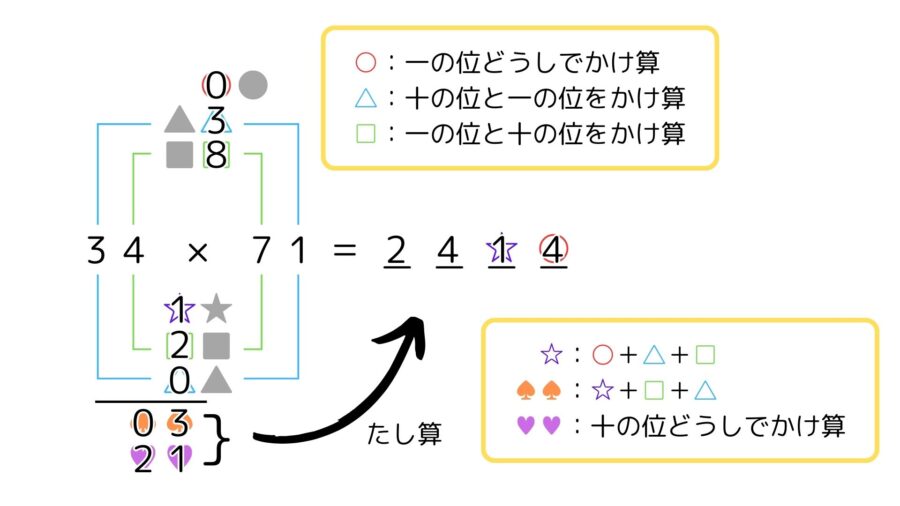
あゆみ算は手順が多いため、慣れるまでは上記の図に数字を当てはめながら計算方法を覚えるのがおすすめです。11×11〜19×19までの計算なら「ラッキーあゆみ算」という方法で、さらに素早く暗算できます。
ラッキーあゆみ算とは「たすかけプレート」という図を活用して計算する方法です。たとえば、13×19をラッキーあゆみ算で計算すると以下3つの手順で答えを出せます。
- 「13」と19の一の位「9」をたす(13+9=22)
- 一の位どうしをかける(3×9=27)
- 22を10倍した数(220)と27をたす(220+27=247)
ラッキーあゆみ算についても、最初から暗算だけに頼らず書く練習を繰り返してコツを掴むことが大切です。
インド式計算
インド式計算も、2ケタどうしのかけ算を暗算するための計算方法です。おみやげ算は、インド式計算の代表的な手法の一つだといわれています。
インド式計算は、数字の組み合わせによって計算方法を変えるのが特徴です。たとえば「十の位が同じかつ一の位の合計が10の場合」は以下の手順で計算します。
【34×36の場合】
| 計算手順 | 計算方法 | 計算式 |
| 手順1 | それぞれの数字を一の位と十の位に分解する | (30+4)×(30+6) |
| 手順2 | 34の「4」を36に加える もしくは 36の「6」を34に加える | 30×(30+6+4)=30×40(=1200) もしくは (30+4+6)×30=40×30(=1200) |
| 手順3 | 一の位どうしの数をかける | 4×6=24 |
| 手順4 | 手順1と手順2で出した数字をたす | 1200+24=1224 |
インド式計算のさまざまな計算法を習得し、問題に合わせて取り入れると複雑な2ケタのかけ算でも簡単に答えを求められます。
まとめ

本記事では、おみやげ算を使った計算方法についてご説明しましたが、特に大切なポイントは以下の3つです。
- おみやげ算を使うと、かけ算の筆算が必要な問題でも少ない負担で効率的に答えを求められる
- おみやげ算を使うときは一定の条件を満たす必要があるため、筆算を使った基本的な計算力を身につけることも大切
- 「なぜこの計算が成り立つのか」という仕組みを理解することで、おみやげ算を正しく活用して素早く正確に計算できる
おみやげ算は計算スピードを上げる便利な手法ですが、九九や「2ケタ×10」「2ケタ×20」の暗算ができなければミスの増加につながります。そのため、日頃から計算練習を繰り返して基礎学力を身につけましょう。
本記事の内容をもとに、お子さんが最適な計算方法を実践し、成績アップや志望校合格に近づけるよう心からお祈り申し上げます。













