植木算はどのように解けばいいのか。植木算の計算方法や公式はどのように使い分ければいいのか。植木算が苦手な場合、どのように克服すればいいのか。
本記事をご覧の方は、中学受験における植木算の重要性や効果的な学習方法について、さまざまな疑問や悩みを抱えていらっしゃるのではないでしょうか。
本記事では、植木算の基礎から応用までを、以下の6点にわたって詳しく解説します。
- 植木算とは何か、なぜ難しいとされるのか
- 植木算の基本的な3つのパターンと解き方
- 中学受験で頻出の応用問題とその対策
- 植木算が苦手な理由と克服法
- 効果的な学習方法と親御さんができるサポート
- 中学受験に向けた塾での学習の重要性
本記事をご覧いただければ、植木算の本質的な考え方から実践的な解法まで体系的に理解できます。中学受験で重要な単元である植木算を得点源にできるよう、ぜひ参考にしてください。
目次
植木算とは

植木算は、小学校の算数で学ぶ重要な単元の一つで、道路沿いやフェンスなどに等間隔で物を配置する際に必要な数を求める計算方法です。
一見シンプルな計算に見えますが、「間の数」と「本数」の関係を正確に理解する必要があり、論理的思考力を測るための最適な設問のひとつとしてしばしば出題されます。また、実生活でも活用できる実用的な計算方法であり、後の数学学習でも重要となる「規則性」や「数列」の基礎となる考え方を学ぶことができます。
特に中学受験では、基本的な植木算の力をもとに、より複雑な応用問題に取り組むことになるため、しっかりとした基礎固めが重要です。
植木算は何年生で習うのか
植木算という言葉自体は学習指導要領には記載されていません。しかし、数学的な考え方や多面的な思考が求められるようになる小学4年生ごろから学習する人が多いでしょう。
4年生の段階では「何個おき」という考え方や、間の数と本数の関係についての理解が求められます。その後、5年生以降も面積計算や比例の問題など、より高度な内容と組み合わさった応用問題として出題されることがあります。
そのため、4年生のうちに基本をしっかり押さえることで、後の複雑な問題にも対応できる力を身につけることが大切です。また、計算力だけでなく図を描いて考える習慣や、問題文を正確に読み取る力も養うようにしましょう。
中学受験で植木算は出題されるのか

中学受験では、植木算の考え方を応用した問題が頻出の単元として出題されます。特に難関校の入試では、単純な植木算の形式ではなく、図形問題や割合の計算と組み合わさった複合問題として出題されることが多いのが特徴です。
たとえば、正方形の土地に木を等間隔で植える問題や、円形の池の周りに花を植える問題など、図形的な感覚と植木算の考え方を組み合わせて解く必要があります。また、時間の経過や速さに関する問題でも、植木算の考え方が応用されることがあります。
入試では、基本的な計算力はもちろん、問題文の読解力、図形的な直感力、そして応用的な思考力まで、総合的な学力を見るための重要な指標として植木算が活用されています。そのため、早い段階から基本パターンをしっかりと理解し、さまざまな応用問題に取り組んでおくことが合格への近道となります。
植木算が難しいと言われる理由

植木算が難しいと言われる理由は、主に次の5つが挙げられます。
- 抽象的で理解が難しいため
- 問題文の読解力が必要なため
- 複数のパターンを使い分ける必要があるため
- 図や絵を描く習慣がないため
- 応用力が求められるため
特に小学生にとって、目に見えない「間」という概念を理解し、それを数式に置き換えるという行程が非常に難しく感じる場合があります。また、問題文から状況を正確に読み取り、適切な解法を選択する必要があることも、多くのお子さんが苦手意識を持つ原因となっています。
抽象的で理解が難しいため
植木算の最大の難関は、「間の数」と「本数」という2つの概念の関係性を理解することです。
たとえば、5本の木があるとき、間の数は4になるという考え方は、小学生にとって非常に抽象的で捉えにくい概念です。さらに、「3本おき」などの表現と実際の間隔の関係も、混乱を招きやすいポイントとなっています。
このような抽象的な概念を理解するためには、具体物を使った説明や、図を描いて視覚化するなどの工夫が必要不可欠です。特に、はじめて植木算を学ぶ段階では、実際に木や人形を並べてみるなど、具体的な体験を通じて理解を深めることが重要です。
問題文の読解力が必要なため
植木算の問題は、通常、文章で状況が説明されるため、高い読解力が求められます。
たとえば、「両端に木を植える」「2メートルおきに植える」「等間隔に並べる」といった表現を正確に理解し、それを数式に変換する必要があります。特に、「おき」という言葉の意味や、「間隔」と「本数」の関係性を正しく把握することが重要です。
また、問題文には解答するために必要な情報がちりばめられているため、重要な数値や条件を見落とさないよう、丁寧に読み解く力が必要です。
これらの要素が組み合わさることで、算数が得意なお子さんでも、読解力が不足していると正解までたどり着けない場合があります。
複数のパターンを使い分ける必要があるため
植木算には「両端を含む」「両端を含まない」「円形」など、複数の基本パターンが存在します。それぞれのパターンで計算方法が異なるため、問題文から適切なパターンを見極める力が必要です。
たとえば、両端を含む場合は「間の数+1」が本数になりますが、両端を含まない場合は「間の数-1」となります。さらに、円形の場合は「間の数=本数」となり、全く異なる計算方法を用います。これらのパターンを正しく判断し、適切な公式を選択することは、多くのお子さんにとって大きな課題となっています。
特に応用問題では、複数のパターンが組み合わさることもあり、より高度な判断力が求められるため、難易度の高い問題になることが多いです。
図や絵を描く習慣がないため
植木算の問題を解く上で、図や絵を描いて状況を視覚化することは非常に重要です。しかし、多くのお子さんは問題を見ただけで計算しようとする傾向があり、図示する習慣が身についていません。
図を描くことで、「間の数」と「本数」の関係が明確になり、どのパターンを使うべきかの判断も容易になります。また、描いた図を使って実際に数えてみることで、計算結果の確認もできます。
図示する習慣がないお子さんは、問題の状況を具体的にイメージすることが難しく、結果として誤答につながりやすくなってしまいます。
応用力が求められるため
中学受験レベルの植木算では、基本パターンを理解しているだけでは対応できない応用問題が多く出題されます。
たとえば、図形の問題と組み合わさったり、時間や速さの概念が加わったりするなど、複数の要素を統合して考える必要があります。また、二次植木算のように、既存の木の間にさらに木を植える問題や、複数の図形が組み合わさった問題なども出題されます。
これらの問題を解くためには、基本的な解法を応用する力や、場面に応じて柔軟に思考を展開する力が必要です。多くのお子さんは、この応用的な思考への移行に苦労し、苦手意識を持ってしまう傾向があります。
植木算の基本問題と解き方

植木算の基本問題は、大きく分けて3つのパターンがあります。
- 両端に木を植えるパターン
- 両端に木を植えないパターン
- 池などの円形に植えるパターン
これらのパターンを正しく理解し、問題文から適切なパターンを選択できるようになることが、植木算をマスターするための第一歩となります。また、それぞれのパターンで公式は異なりますが、必ず図を描いて確認する習慣をつけることで、ミスを防ぐことができます。
両端に木を植えるパターン
両端に木を植えるパターンは、植木算の最も基本的な形式です。
たとえば、次のような問題がこのパターンに該当します。
| 道路に沿って2メートルおきに木を植えます。道路の長さは10メートルです。両端にも木を植える場合、必要な木の本数を求めなさい。 |
このパターンでは、「間の数+1=木の本数」という公式を使います。
今回の例題では以下の手順で計算します。
- まず道路の長さ(10m)を間隔(2m)で割って、間の数を求めます。10÷2=5(間)
- 両端に木を植えるので、間の数に1を足します。5+1=6(本)
この際、必ず図を描いて確認することをおすすめします。
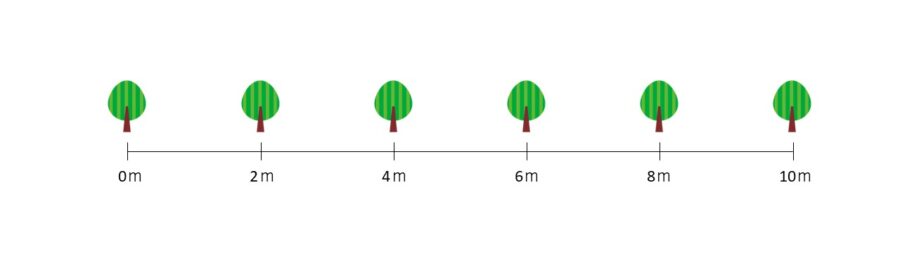
図を描くことで、たとえば10mの道路に2mおきに木を植えると、0m、2m、4m、6m、8m、10mの位置に木が来ることが視覚的に理解でき、合計6本必要だということが一目で分かります。
また、この考え方は街頭や花壇などさまざまな日常的な場面で応用されています。そのため、日頃の生活の中でも目にすることが多く、意識して観察することで問題を解く際にもイメージしやすくなります。
計算する前に「両端には必ず木(または物)が来る」ということを意識することで、間違いを防ぐことができるでしょう。特に受験では、問題文をよく読んで「両端に植える」という条件を見落とさないようにすることが重要です。
両端に木を植えないパターン
両端に木を植えないパターンは、たとえば次のような問題です。
| フェンスの支柱を等間隔に立てます。フェンスの長さは12メートルで、3メートルおきに支柱を立てます。両端に支柱を立てない場合、必要な支柱の本数を求めなさい。 |
このパターンでは、「間の数-1=木の本数」という公式を使います。計算の手順は以下の通りです。
- フェンスの長さ(12m)を間隔(3m)で割って、間の数を求めます。12÷3=4(間)
- 両端に支柱を立てないので、間の数から1を引きます。4-1=3(本)
この場合も図を描いて確認すると、3m、6m、9mの位置に支柱が必要になることが分かります。
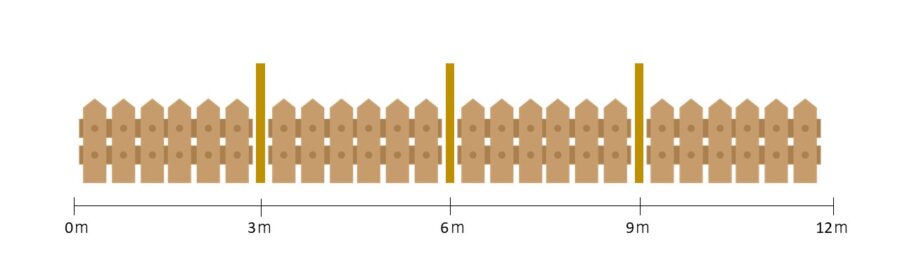
このように図示することで、なぜ間の数から1を引くのかが直感的に理解できるようになります。また、答えの確認もしやすくなります。
このパターンでよくある間違いは、両端に支柱を立てない場合でも「間の数+1」の公式を使ってしまうことです。
身の回りの具体例でも、壁や建物に支柱を取り付ける場合は両端の支柱が不要になることがあるため、普段から両端に支柱がある場合とない場合を意識しながら生活すると問題を解く際にも見逃しが防げるためおすすめです。
池などの円形に植えるパターン
円形に植えるパターンは、たとえば次のような問題が挙げられます。
| 円形の池の周りに3メートルおきに花を植えます。池の外周は18メートルです。必要な花の本数を求めなさい。 |
このパターンの特徴は、「間の数=木の本数」という公式を使うことです。これは、円形の場合、最初の位置に戻ってくるため、両端という概念がなくなるためです。計算の手順は以下の通りです。
- 池の外周(18m)を間隔(3m)で割ります。18÷3=6(本)
円形の問題では、特に図を描くことが重要です。円周上に等間隔で点を打っていくことで、最後の花と最初の花の間も他の間隔と同じになることが視覚的に理解できます。
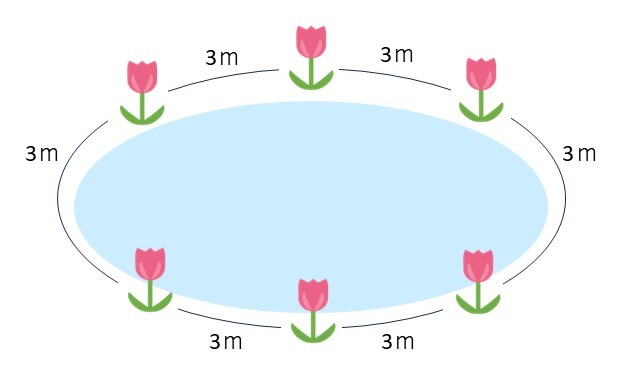
また、この考え方は、正多角形の頂点の数を求める問題にも応用できます。正多角形の場合は、以下の点に注意が必要です。
- 正多角形の周りの長さを先に求める
- 各頂点にも植える場合は、頂点の位置も考慮する
このように、円形や正多角形の問題では、図形の特徴を理解し、全体の長さと間隔の関係に着目することが重要です。
植木算の応用問題と解き方

植木算の基本パターンを理解したら、次は応用問題に挑戦していきましょう。応用問題は中学受験でよく出題され、次のような問題が代表として挙げられます。
- 二次植木算
- 面の植木算
- 複合図形の植木算
- 時間の植木算
- のりしろ問題
これらの問題は、基本の考え方を応用しながら、より複雑な状況に対応する力を養うことが大切です。難しく感じる問題でも、図を描いて基本パターンに分解することで、解きやすくなります。
二次植木算
二次植木算は、既に植えられた木の間に、さらに新しい植物を植えていく問題です。たとえば、次のような問題が出題されます。
| 道路に沿って4メートルおきに木が植えられています。この木と木の間に2メートルおきに花を植えることにしました。道路の長さは20メートルで、両端にも木があります。新たに必要な花の本数を求めなさい。 |
この問題を解くポイントは、以下の手順で考えることです。
- まず、既存の木の配置を図に描きます。(4mおき、両端含む)
- 木の本数を求めます。20÷4+1=6(本)
- 木と木の間(4m)に、何本の花が植えられるか考えます。4÷2-1=1(本)
- 木の間の数(木の本数-1)に、一つの間に植える花の本数をかけます。(6-1)×1=5(本)
この例題のような「4メートルおきの木の間に2メートルおきに花を植える」問題では、最初に木の配置をしっかり図示することが大切です。図を描く際のコツは、まず数直線を引き、木の位置に○、花の位置に×など、異なる記号を使うことです。
また、間違いやすいポイントとして、最初の間隔(4m)と二次的な間隔(2m)の関係を見間違えてしまう場合があります。そのため、問題文をしっかりと読み解き、情報を正確に理解することが大切です。これは植木算の基本であり、応用問題でも常に意識する必要があるでしょう。
面の植木算
面の植木算は、長方形や正方形の土地に格子状に木を植える問題です。たとえば、次のような問題です。
| 縦12メートル、横15メートルの長方形の土地に、縦横とも3メートルおきに木を植えます。四隅にも木を植える場合、必要な木の本数を求めなさい。 |
この種の問題は、以下の手順で解きます。
- 縦方向の木の本数を求めます。12÷3+1=5(本)
- 横方向の木の本数を求めます。15÷3+1=6(本)
- 縦と横の本数をかけ合わせます。5×6=30(本)
面の植木算では、縦と横それぞれで「両端に木を植えるパターン」の考え方を使います。また、格子点の数を求める問題としても捉えることができ、図形の問題との関連も深いため、さまざまな場面で応用が利きます。
例題の「縦12メートル、横15メートル」の問題では、計算手順を「縦→横→掛け算」と明確に分けることで、ミスを防ぐことができます。特に重要なのは、「四隅にも木を植える→両端を含む→+ 1にする」という基本の流れをしっかり理解することです。
実際の試験では、土地の形は同じでも、「四隅を除く」「外周のみ」といった条件が追加されることがあります。その場合は、まず基本の総本数を求めてから、条件に応じて本数を調整するとよいでしょう。
複合図形の植木算
複合図形の植木算は、L字型やT字型など、単純な長方形や正方形ではない形状の土地や道路に木を植える問題です。たとえば、次のような問題を指します。
| L字型の道路に沿って3メートルおきに街灯を設置します。道路の形は、縦が20メートル、横が15メートル、幅は考えないものとします。両端にも街灯を設置する場合、必要な街灯の本数を求めなさい。 |
この問題の解き方のポイントは以下の通りです。
- 複合図形を単純な図形に分解します。(この場合、縦と横の部分)
- それぞれの部分で植木算を行います。
- 重複する部分(この場合、角の街灯)を調整します。
実際に計算してみると次のようになります。
- 縦の部分:20÷3+1=7(本)
- 横の部分:15÷3+1=6(本)
- 角の部分で1本重複するので:7+6-1=12(本)
このように、複雑な形状でも、基本パターンに分解して考えることで解決できます。
L字型の例題で学んだ「分解して考える」という方法は、どんな複雑な形状でも対応できる基本テクニックです。ただし、分解した後の重複部分の処理で間違いやすいため、先ほどの解き方のポイントをしっかり意識しましょう。
特に重要なのは、分解した図形の接点となる部分を二重に数えないよう、しっかりチェックすることです。
時間の植木算
時間の植木算は、時間の経過や定期的なイベントを植木算の考え方で解く問題です。たとえば、次のような問題です。
| 1時間おきに発車する電車があります。始発は午前6時、最終は午後11時です。この電車は1日に何本運行されますか。 |
解き方のポイントは以下の通りです。
- 時間の間隔を「間」として考えます。
- 始発と最終の時刻から全体の時間を求めます。
- 通常の植木算と同じように考えます。
今回の例を実際に計算してみると
- 6時(午前6時)から23時(午後11時)までは17時間
- 1時間おきで、始発と最終を含む
- 17÷1+1=18(本)
時間の植木算では、時刻を数直線上に表すと理解しやすくなります。
例題の「午前6時から午後11時まで1時間おき」という問題では、時刻の範囲を正確に把握することが重要です。
特に時間の植木算で最も気をつけたいのは、時刻の表記方法です。計算の際は、必ず24時間表記に統一することが重要なポイントになります。この例題なら、午前6時→6時、午後11時→23時と変換できます。
また、時間の区切り方は通常の植木算と同じ考え方が使えます。(終了時刻-開始時刻)÷間隔で割って「+1」を忘れないようにしましょう。
のりしろ問題
のりしろ問題は、紙をつなぎ合わせる際の重なる部分を植木算の考え方で解く問題です。たとえば、次のような問題が出題されます。
| 長さ30センチメートルの紙を3枚つなぎ合わせます。つなぎ目は5センチメートルずつ重ねます。できあがった紙の長さを求めなさい。 |
この問題を解くにあたっては、次の点に注意が必要です。
- 紙の枚数から、のりしろ(重なる部分)の数を考えます。
- 全体の長さから重なる部分を引きます。
- のりしろの数は、紙の枚数より1つ少なくなることに注意します。
例題を計算すると次のようになります。
- 3枚の紙の合計:30×3=90(センチメートル)
- のりしろの数:3-1=2(カ所)
- のりしろの合計:5×2=10(センチメートル)
- 完成した長さ:90-10=80(センチメートル)
このように、のりしろ問題も植木算の考え方を応用して解くことができます。図を描いて確認することで、より理解が深まります。
例題の「30センチメートルの紙を3枚、のりしろ5センチメートル」という問題の考え方は、多くの応用問題に活用できます。のりしろ問題で大切なのは、「重なる部分」を正確に把握することです。紙をつなぐ作業をイメージしながら、以下の点を確認しましょう。
- のりしろの数は必ず(紙の枚数-1)になる
- 重なる部分は全体の長さから引く
- 両端をつなげる(リング上にする)設問もある
このパターンの場合でも、基本問題同様「図を描く」「問題をよく読む」といったことが重要になります。
植木算の効果的な学習法

植木算を素早く解けるようになるためには、以下のポイントを意識して学習を進める必要があります。
- 視覚化することを重視して学習する
- 基本から段階的に学習する
- 具体的な実体験から理解を深める
- 毎日少しずつ練習する
- 読解力を向上させる
- 親御さんが理解度をチェックする
ここでは、これらのポイントについて詳しく解説していきます。
視覚化することを重視して学習する
植木算の学習では、抽象的な概念を具体的にイメージできるようにすることが重要です。まずは、実際に消しゴムや鉛筆などを並べて、間の数と本数の関係を体感的に理解しましょう。
また、すべての問題で必ず線分図や絵を描く習慣をつけることで、問題の状況が明確になり、解き方の見通しも立ちやすくなります。特に応用問題では、図を描くことで複雑な状況も整理でき、どのパターンを使うべきかの判断も容易になります。
図を描く際は、単に木や花を点で表すだけでなく、間隔を示す矢印や数値も書き込むと良いでしょう。このように、視覚的な要素を積極的に取り入れることで、計算の意味や解法の本質的な理解につながります。
こうした視覚化の習慣は、植木算に限らず中学受験全体でも大きな武器となるでしょう。
基本から段階的に学習する
植木算の学習は、基本的なパターンの理解から始めることが大切です。
最初は「両端を含む」「両端を含まない」「円形」という3つの基本パターンを、それぞれ小さな数字を使って練習します。その後、各パターンの特徴や公式を理解できたら、少しずつ数字を大きくしていきましょう。
基本パターンが定着してから、二次植木算や面の植木算などの応用問題に進むことで、無理なく実力を伸ばすことができます。また、同じパターンの問題を繰り返し解くことで、解法が自然と身についていきます。
特に重要なのは、ステップアップの際に焦らないことです。たとえば、基本パターンでは5や10など計算しやすい数字から始め、徐々に7や13などの素数を含む問題に移行するなど、細かく難易度を調整するのも効果的です。
各段階で十分な練習時間を確保することで、より確実な理解が期待できます。
具体的な実体験から理解を深める
植木算の抽象的な概念を理解するには、実際の生活場面と結びつけることが効果的です。
たとえば、公園のベンチの配置や、教室の机の並び方など、身近な例を観察することで、等間隔に並べるということの意味が実感として分かってきます。また、家庭でも、おもちゃを等間隔に並べる練習をしたり、散歩中に街路樹の間隔を数えたりすることで、自然と植木算の感覚が身についていきます。
このように日常生活の中で「等間隔」や「間の数」を意識することで、問題を解く際にもイメージが湧きやすくなります。さらに、実際に物を並べる体験は、空間認識能力の向上にもつながります。
このような実体験を通じた学習は、特に低学年のお子さんに有効な方法です。
毎日少しずつ練習する
植木算の上達には、コツコツとした練習が欠かせません。
1日1問でも良いので、継続的に問題を解く習慣をつけましょう。最初は基本的なパターンの問題から始め、徐々に応用問題に挑戦していきます。間違えた問題は、なぜ間違えたのかを必ず確認し、同じミスを繰り返さないようにすることが大切です。
また、問題を解く際は時間を計りながら解くことで、中学受験本番でも余裕を持って解けるようになります。
さらに、定期的に過去に解いた問題を見直すことも効果的です。特に苦手だった問題や間違えやすかったパターンを振り返ることで、理解が深まっていくでしょう。このとき、解答時間を記録していくと、自分の成長を実感でき、モチベーション維持にもつながります。
読解力を向上させる
植木算の問題を正確に解くためには、問題文を丁寧に読み解く力が必要です。
問題文を読む際は、「両端」「間隔」「等間隔」などの重要なキーワードに注目し、それらの言葉が持つ意味を正確に理解することが大切です。また、問題文に出てくる数値や条件を見落とさないよう、ゆっくりと読む習慣をつけましょう。
読解力は他の単元でも必要となる基礎的な力なので、国語の学習と併せて強化していくのがおすすめです。特に、問題文中の「~おきに」「~ずつ」といった表現の違いを理解することが重要です。
学習の際は問題文を音読したり、キーワードに線を引いたりする習慣をつけることで、正確な読解力が身についていきます。
親御さんが理解度をチェックする
親御さんが家庭でお子さんの学習をサポートする際は、単に答えを確認するだけでなく、解き方を説明させることが効果的です。
説明させることで、理解が不十分な部分が明らかになり、どこでつまずいているのかが分かります。また、間違えた問題については、なぜその間違いが起きたのかを一緒に分析し、正しい解き方に気づけるよう導いていきましょう。
お子さんの理解度に合わせて適切な難易度の問題を選ぶことも、学習効果を高めるポイントです。定期的に復習テストを実施することで、どの程度理解が定着しているかを確認できます。
また、お子さんが自信を持てるよう、できたことを積極的に褒めることも大切です。特に、新しい解法を発見したり、効率的な解き方を考え出したりした際は、そのがんばりを認めてあげることで、数学的思考力の向上につながります。
中学受験対策をするには塾に通うことがおすすめ

中学受験レベルの植木算を独学で習得するのは、多くのお子さんにとって大きな関門となります。そのため、可能であれば塾に通うことをおすすめします。
中学受験のノウハウが蓄積された塾では、長年の指導経験をもとに体系化された効果的な学習方法が用意されており、つまずきやすいポイントに対する具体的な対策も準備されています。
また、基本問題から応用問題まで、お子さんの理解度に合わせた豊富な演習問題が用意されているため、無理なく実力を伸ばすことができます。特に、入試本番で頻出の複合問題や時間配分については、プロの講師による的確なアドバイスが不可欠です。
さらに、塾で行われる模擬試験などを通じて自分の実力を客観的に把握し、効率的に弱点を克服することができます。植木算は中学受験の重要単元の一つですので、早めに塾の指導を受けることで、受験本番での得点源として確実に活用できるようになるでしょう。
まとめ

本記事では、中学受験における植木算の重要性や効果的な学習方法についてご説明しましたが、特に大切なポイントは以下の3つです。
- 植木算は抽象的な概念理解と正確な読解力が必要で、多くのお子さんが苦手意識を持ちやすい単元
- 基本の3パターン(両端を含む、両端を含まない、円形)をしっかり理解し、必ず図を描いて考える習慣をつけることが重要
- 効果的な学習のためには視覚化を重視し、具体物を使った体験から理解を深め、基本から応用へと段階的に進むことがおすすめ
植木算は中学受験で頻出の単元であり、基本問題から応用問題まで幅広く出題されます。特に難関校では、図形問題や時間の問題と組み合わさった複合問題として出題されることも多いため、早い段階から計画的な学習が必要です。
本記事の内容をもとに、お子さんが植木算の基礎から応用まで確実に理解し、中学受験の合格に向けて着実に力をつけられることを心からお祈り申し上げます。













